multiplicação e divisão de radicais

Radicais

OPERAÇÕES COM RADICAIS

RADICAIS SEMELHANTES
Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando

Exemplos de radicais semelhantes

a) 7√5 e -2√5
b) 5³√2 e 4³√2

Exemplos de radicais não semelhantes

a) 5√6 e 2√3
b) 4³√7 e 5√7



ADIÇÃO E SUBTRAÇÃO

1º CASO : Os radicais não são semelhantes
Devemos proceder do seguinte modo:

a) Extrair as raízes (exatas ou aproximadas)
b) Somar ou subtrair os resultados

Exemplos

1) √16 + √9 = 4 + 3 = 7
2) √49 - √25 = 7 – 5 = 2
3) √2 + √3 = 1,41 + 1,73 = 3,14

Neste último exemplo, o resultado obtido é aproximado, pois √2 e √3 são números irracionais (representação decimal infinita e não periódica)

EXERCÍCIOS

1) Calcule

a) √9 + √4 = 5
b) √25 - √16 = 1
c) √49 + √16 = 11
d) √100 - √36 = 4
e) √4 - √1 = 1
f) √25 - ³√8 = 3
g) ³√27 + ⁴√16 = 5
h) ³√125 - ³√8 = 3
i) √25 - √4 + √16 = 7
j) √49 + √25 - ³√64 = 8


2º CASO: Os radicais são semelhantes.

Para adicionar ou subtrair radicais semelhantes, procedemos como na redução de termos semelhantes de uma soma algébrica.

Exemplos:

a) 5√2 + 3√2 = (5+3)√2 = 8√2
b) 6³√5 - 2³√5 = (6 – 2) ³√5 = 4³√5
c) 2√7 - 6√7 + √7 = (2 – 6 +1) √7 = -3√7

EXERCÍCIOS

1) Efetue as adições e subtrações:

a) 2√7 + 3√7 = 5√7
b) 5√11 - 2√11 = 3√11
c) 8√3 - 10√3 = -2√3
d) ⁴√5 + 2⁴√5 = 3⁴√5
e) 4³√5 - 6³√5 = -2³√5
f) √7 + √7 = 2√7
g) √10 + √10 = 2√10
h) 9√5 + √5 = 10√5
i) 3.⁵√2 – 8.³√2 = -5.³√2
j) 8.³√7 – 13.³√7 = -5.³√7
k) 7√2 - 3√2 +2√2 = 6√2
l) 5√3 - 2√3 - 6√3 = -3√3
m) 9√5 - √5 + 2√5 = 10√5
n) 7√7 - 2√7 - 3√7 = 2√7
o) 8. ³√6 - ³√6 – 9. ³√6 = -2. ³√6
p) ⁴√8 + ⁴√8 – 4. ⁴√8 = -2. ⁴√8

3º CASO: Os radicais tornam-se semelhantes depois de simplificados.

Exemplos

a)5√3 + √12
..5√3 + √2².3
..5√3 + 2√3
..7√3

b)√8 + 10√2 - √50
..√2².√2 +10√2 - √5². √2
..2√2 + 10√2 - 5√2
..7√2

EXERCÍCIOS

1) Simplifique os radicais e efetue as operações:

a) √2 + √32= 5√2
b) √27 + √3 = 4√3
c) 3√5 + √20 = 5√5
d) 2√2 + √8 = 4√2
e) √27 + 5√3
f) 2√7 + √28 = 4√7
g) √50 - √98 = -2√2
h) √12 - 6√3 = -4√3
i) √20 - √45 = -√5

2) Simplifique os radicais e efetue as operações:

a) √28 - 10√7 = -8√7
b) 9√2 + 3√50 = 24√2
c) 6√3 + √75 = 11√3
d) 2√50 + 6√2 = 16√2
e) √98 + 5√18 = 22√2
f) 3√98 - 2√50 = 11√2
g) 3√8 - 7√50 = -29√2
h) 2√32 - 5√18 = -7√2

3) Simplifique os radicais e efetue as operações:

a) √75 - 2√12 + √27 = 4√3
b) √12 - 9√3 + √75 = -2√3
c) √98 - √18 - 5√32 = -16√2
d) 5√180 + √245 - 17√5 = 20√5



MULTIPLICAÇÃO E DIVISÃO

1º Caso: Os radicais têm o mesmo índice
Efetuamos a operação entre os radicandos

Exemplos:

a) √5 . √7 = √35
b) 4√2 . 5√3 = 20√6
c) ⁴√10 : ⁴√2 = ⁴√5
d) 15√6 : 3√2 = 5√3

2º Caso: Os radicais não têm o mesmo índice
Inicialmente devemos reduzi-los ao mesmo índice

Exemplos

a) ³√2 . √5 = ⁶√2² . ⁶√5³ = ⁶√4 . ⁶√125 = ⁶√500


b)⁵√7 : √3 = ¹⁰√7² : ¹⁰√3⁵ = ¹⁰√49/243


EXERCÍCIOS

1) Efetue as multiplicações e divisões:

a) √2 . √7 = √14
b) ³√5 . ³√10 = ³√50
c) ⁴√6 . ⁴√2 = ⁴√12
d) √15 . √2 = √30
e) ³√7 . ³√4 = ³√28
f) √15 : √3 = √5
g) ³√20 : ³√2 = ³√10
h) ⁴√15 : ⁴√5 = ⁴√3
i) √40 : √8 = √5
j) ³√30 : ³√10 = ³√3

2) Multiplique os radicais e simplifique o produto obtido:

a) √2 . √18 = 6
b) √32 . √2 = 8
c) ⁵√8 . ⁵√4 = 2
d) ³√49 . ³√7 = 7
e) ³√4 . ³√2 = 2
f) √3 . √12 = 6
g) √3 . √75 = 15
h) √2 . √3 . √6 = 6

3) Efetue as multiplicações e divisões:

a) 2√3 . 5√7 = 10√21
b) 3√7 . 2√5 = 6√35
c) 2. ³√3 . 3. ³√3 = 6. ³√15
d) 5.√3 . √7 = 5√21
e) 12. ⁴√25 : 2. ⁴√5 = 6. ⁴√5
f) 18. ³√14 : 6. ³√7 = 3. ³√2
g) 10.√8 : 2√2 = 5√4

SISTEMAS DE EQUAÇÕES

SISTEMAS DE EQUAÇÕES DO 2º GRAU

 Observe o seguinte problema:

 Uma quadra de tênis tem a forma da figura, com perímetro de 64 m e área de 192 m². Determine as medidas x e y indicadas na figura.

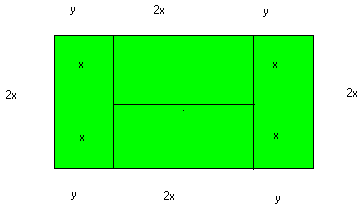
De acordo com os dados, podemos escrever:

8x + 4y = 64

2x . ( 2x + 2y) = 192 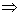  4x² + 4xy = 192

Simplificando, obtemos:

2x + y = 16                 1

x² +xy = 48                 2

Temos aí um sistema de equações do 2º grau, pois uma das equações é do 2º grau.

Podemos resolvê-lo pelo método a substituição:

Assim:    2x + y = 16        1

                        y = 16 - 2x

Substituindo y em  2 , temos:

               x² + x ( 16 - 2x) = 48

              x ² + 16x - 2x² = 48

                - x²  + 16x - 48 = 0 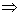 Multiplicando ambos os membros por -1.

                  x² - 16x + 48 = 0

x'=4       e        x''=12

Determinando y para cada um dos valores de x, obtemos:

y'=16 - 2 . 4 = 8

y''=16 - 2 . 12 = - 8

As soluções  do sistema são os pares ordenados (4,8) e ( 12, -8).

desprezando o par ordenado que possui ordenada negativa, teremos para dimensões da quadra:

                    Comprimento    =2x + 2y = 2.4 + 2.8 = 24m

                    Largura              =2x = 2. 4 = 8m

Verifique agora a solução deste outro sistema:

   

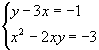
Isolando y em 1

               y - 3x = -1 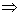 y = 3x - 1

Substituindo em  2

           x²  - 2x(3x - 1)  = -3

           x² - 6x² + 2x    = -3   

          -5x² + 2x + 3    = 0 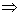   Multiplicando ambos os membros por -1.

           5x² - 2x - 3     = 0

x'=1       e    x''=-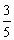

Determinando y para cada um dos valores de x, obtemos:

                                            

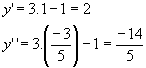
As soluções do sistema são os pares ordenados ( 1, 2) e  .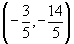

Logo, temos para conjunto verdade: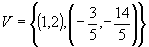 

Equações irracionais

EQUAÇÕES IRRACIONAIS

Considere as seguintes equações:

Observe que todas elas apresentam variável ou incógnita no radicando. Essas equações sãoirracionais.

Ou seja:

     

Equação irracional é toda equação que tem variável no radicando.

 RESOLUÇÃO DE UMA EQUAÇÃO IRRACIONAL

         A resolução de uma equação irracional deve ser efetuada procurando transformá-la inicialmente numa equação racional, obtida ao elevarmos ambos os membros da equação a uma potência conveniente.

         Em seguida, resolvemos a equação racional encontrada e, finalmente, verificamos se as raízes da equação racional obtidas podem ou não ser aceitas como raízes da equação irracional dada ( verificar a igualdade).

       É necessária essa verificação, pois, ao elevarmos os dois membros de uma equação a uma potência, podem aparecer na equação obtida raízes estranhas à equação dada.

Observe alguns exemplos de resolução de equações irracionais no conjunto dos reais.

• 

Solução

                  

Logo, V= {58}.

• 

Solução

                

Logo, V= { -3}; note que 2 é uma raiz estranha a essa equação irracional.

• 

Solução

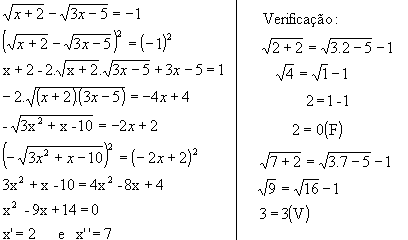
Logo, V= { 7 }; note que 2 é uma raiz estranha a essa equação irracional.

• 

Solução

          

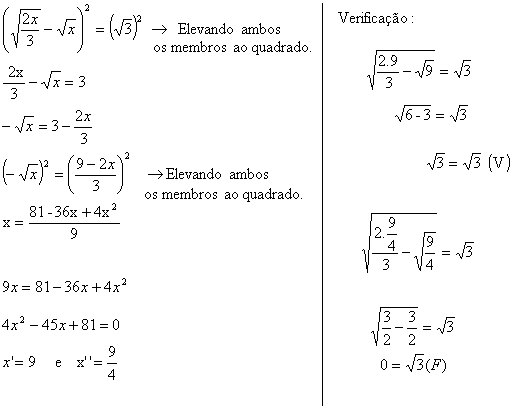
Logo, V={9}; note que 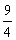 é uma raiz estranha a essa equação irracional.

Equações binoquadradas

Equações biquadradas é uma equação escrita da seguinte forma geral: ax⁴ + bx2 + c = 0. Para resolver (encontrarmos as sua raízes) é preciso transformá-las em uma equação do segundo grau. 

Para melhor compreensão veja no exemplo abaixo como essa transformação acontece e como chegamos às raízes da equação biquadrada. 

y⁴ – 10y² + 9 = 0 → equação biquadrada 

(y²)² – 10y² + 9 = 0 → também pode ser escrita assim. 

Substituindo variáveis: y² = x, isso significa que onde for y² iremos colocar x. 

x² – 10x + 9 = 0 → agora resolvemos essa equação do 2º grau encontrando x` e x`` 

a = 1    b = -10     c = 9 

∆ = b² – 4ac 
∆ = (-10)² – 4 . 1 . 9 
∆ = 100 – 36 
∆ = 64 

x = - b ± √∆             2a 

x = -(-10) ± √64 
             2 . 1 

x = 10 ± 8 
           2 

x’ = 9

x” = 1 

Essas são as raízes da equação x² – 10x + 9 = 0, para encontrarmos as raízes da equação biquadrada y⁴– 10y2 + 9 = 0 devemos substituir os valores de x’ e x” em y² = x. 

Para x = 9 
y² = x 
y² = 9 
y = √9 
y = ± 3 

Para x = 1 
y² = x 
y² = 1 
y = √1 
y = ±1 

Portanto, a solução da equação biquadrada será: 

S = {-3, -1, 1, 3}.

Equações fracionárias

EQUAÇÃO FRACIONÁRIA DO 2º GRAU

Nessas equações (há incógnita no denominador) devemos garantir que nenhum dos denominadores se anule

Exemplo:

Vejamos, através de exemplos, como se resolvem as equações fracionárias.

exemplo 1

Resolver em R a equação x + 1/(x -3) = 5 sendo x diferente 3

Solução:

substituindo na fórmula

exemplo 2

EXERCÍCIOS

1) Resolva a equação do 2º grau em R:

Equações literais de 2° grau

As equações literais do 2º grau são conhecidas por possuírem os coeficientes representados por letras. Esse modelo de equação é utilizado no intuito de aprimorar o desenvolvimento da expressão de Bhaskara, dado os coeficientes numéricos das equações de 2º grau. Dessa forma, ao iniciar esse conteúdo, trabalhe a resolução desse modelo de equação, lembrando que uma equação literal possui como solução uma relação de dependência entre a incógnita e o coeficiente literal.

Apresente exemplos de equações literais do 2º grau e os coeficientes relacionados à incógnita da equação. Veja:

x² – 7ax + 10a² = 0 (a > 0)
Coeficientes:
a = 1
b = –7a
c = 10a²

x² – (m + 3)x + 3m = 0 (m > 3)
Coeficientes:
a = 1
b = m + 3
c = 3m

x² + 8mx = 0
Coeficientes:
a = 1
b = 8m
c = 0

px² – 4x + 4px = 0 (p ≠ 0)
Coeficientes:
a = p
b = –4x
c = 4p

Apresente modelos de equações literais resolvidas utilizando o método de Bhaskara para as equações completas e os métodos da fatoração para as incompletas.

Incompleta

x² + 8mx = 0 (aplicar fator comum em evidência)
x * (x + 8m) = 0

x’ = 0

x + 8m = 0
x’’ = –8m

Conjunto Solução: {x’ = 0 e x’’ = –8m}

Completa

x² – 3ax + 2a² = 0 (a > 0)

a = 1, b = –3a e c = 2a²

∆ = b² – 4ac
∆ = (–3a)² – 4 * 1 * 2a²
∆ = 9a² – 8a²
∆ = a²

Conjunto Solução: {x’ = 2a e x’’ = a}